差分確率

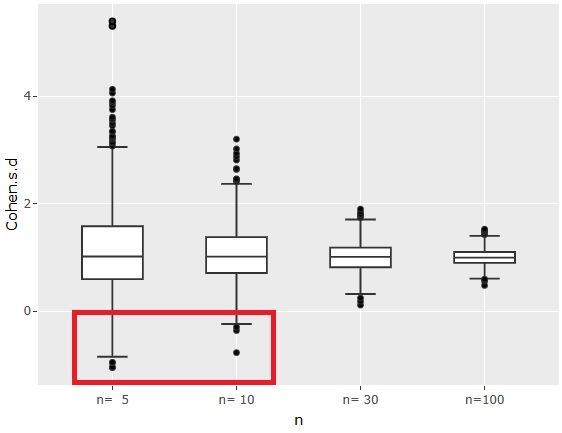
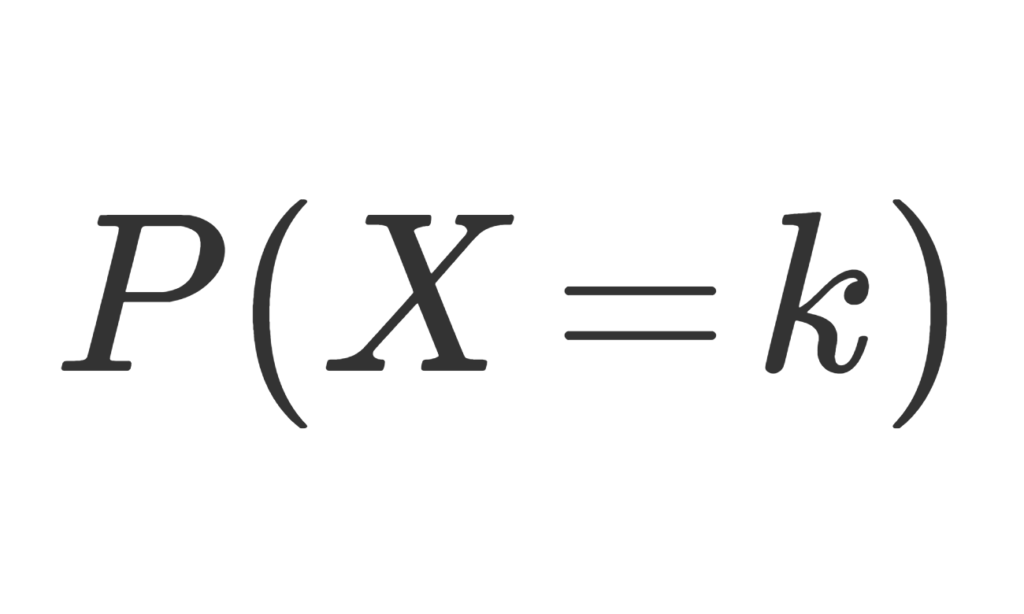差分確率（さぶんかくりつ、Differential Probability）とは、ある有限種類の入力を持つ全射の関数${\displaystyle f(x)}$があったときに、任意の${\displaystyle x}$について、${\displaystyle f(x)\oplus {}f(x\oplus \Delta {}x)}$がある値${\displaystyle \Delta {}y}$になる確率である。${\displaystyle x}$の値域に矛盾しないすべての${\displaystyle \Delta {}x}$に対して${\displaystyle \Delta {}y}$の確率を求めることができる。 ただし、${\displaystyle \Delta {}x=0}$の場合必ず${\displaystyle \Delta {}y=0}$となる。

${\displaystyle \Delta {}x=0}$を除いて、差分確率の中で最も高い確率をその関数の最大差分確率と呼ぶ。 最大差分確率を求めるための計算量は、${\displaystyle x}$の種類のおよそ2乗となる。

差分確率は、ブロック暗号の解読法の一つである差分解読法に用いられる。 ただし、ブロック暗号全体の最大差分確率を求めるための計算量はブロック暗号全体の計算量よりも大きいため、通常は求めることができない。 そのため、ブロック暗号を解読する場合は、小さなブロック単位での最大差分確率を求め、その確率を次のブロックに接続していくことによって全体の差分確率を概算する。このように求めた値は最大差分特性確率と呼ばれ、最大差分確率よりも小さい。

最大差分特性確率の逆数が解読に必要な平文数となる。逆に言えば、最大差分特性確率がブロック長${\displaystyle B}$に対して${\displaystyle 2^{-B}}$より小さければ、差分解読法でその暗号が解読されることはない。

関連項目

• ブロック暗号
• 差分解読法
• 共通鍵暗号
• 暗号理論
• Feistel構造
• SPN構造